Hej!
Jag har fastnat lite och skulle uppskatta lite stöttning. Jag bifogar min uppgift.
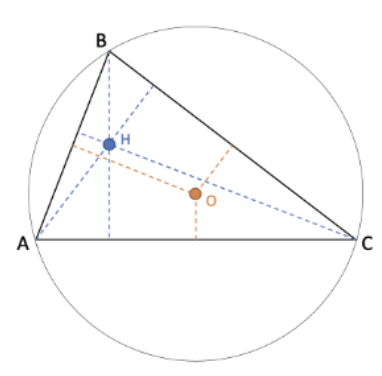
EDIT: Då jag inte kan se att bilden bifogas: Det gäller uppgift 8.15 i boken.
Jag har försökt med ledvis addition, flytta över termer med variabler till VL för att enbart ha konstanter i HL. Sedan har jag försökt att expandera uttryck samt faktorisera.
Jag stirrar mig blind på vad jag har just nu:
4(a-b+c) + 4(-ab-bc+ac) = 49
Detta är enbart en av mina påbörjade "lösningsvägar". Jag tenderar att hamna i liknande lägen var gång.
Jag tycker mig se lite mönster emellanåt, men kör fast. I till exempel:
2a - 2b - 4ab = 29
vill jag gärna trolla lite med VL för att få till en kvadratkomplettering, men ser inte riktigt hur.
Jag önskar självklart ingen lösning här, men hade uppskattat tips på hur jag ska attackera problemet.
Mvh,
Niklas

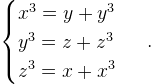
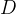
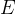
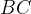
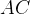
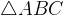
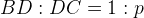
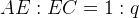
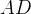
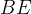
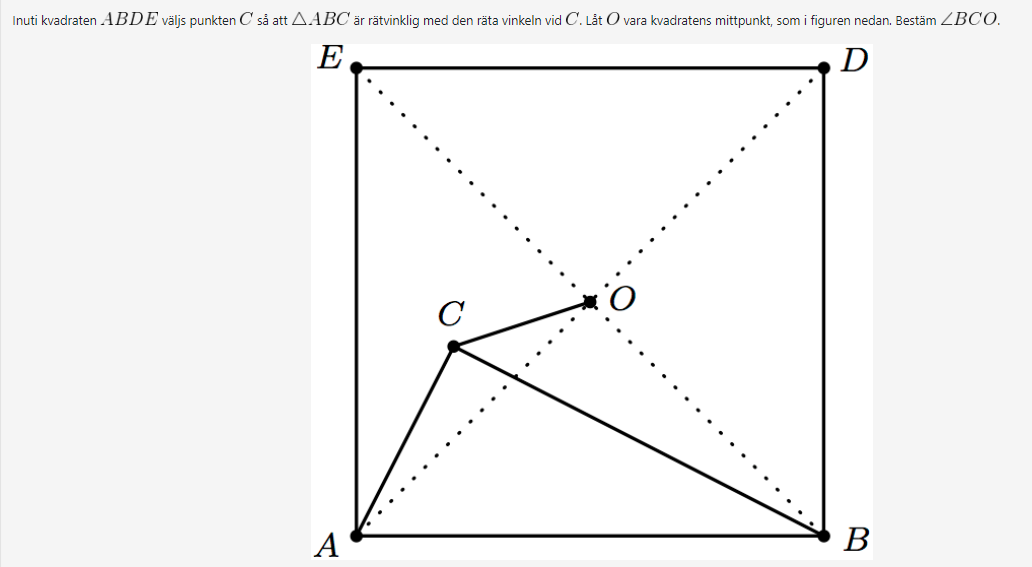
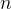
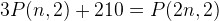
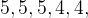
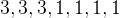
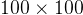 -rutnät. I tur och ordning lägger de ut pjäser som i Xaviers fall är i form av en
-rutnät. I tur och ordning lägger de ut pjäser som i Xaviers fall är i form av en 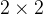 -kvadrat och i Yngves fall i form av bokstaven L formad av tre ihoplimmade småkvadrater. De småkvadrater som bildar dessa två former är förstås lika stora som kvadraterna i nätet. Den som inte längre finner plats för sin pjäs på nätet förlorar spelet.
-kvadrat och i Yngves fall i form av bokstaven L formad av tre ihoplimmade småkvadrater. De småkvadrater som bildar dessa två former är förstås lika stora som kvadraterna i nätet. Den som inte längre finner plats för sin pjäs på nätet förlorar spelet.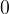
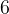
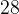
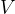
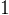
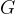
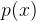 sådant att
sådant att 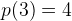 och
och 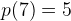 ?
?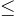 200. Visa att om man beräknar parvisa differenser mellan dessa tal (större tal minus mindre tal), måste man minst en gång få en differens lika med 4 eller 5 eller 9.
200. Visa att om man beräknar parvisa differenser mellan dessa tal (större tal minus mindre tal), måste man minst en gång få en differens lika med 4 eller 5 eller 9.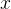 , typ 2:
, typ 2: 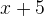 och typ 3:
och typ 3: 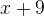 , för alla
, för alla 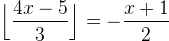 ,
,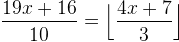 .
.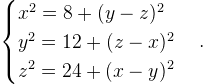

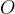
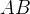

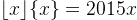
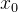
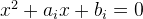
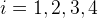
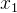
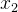
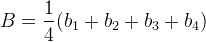
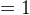 och
och 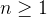 punkter,
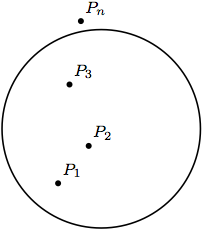
punkter, 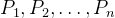 . Visa att man på cirkelns periferi kan finna en punkt
. Visa att man på cirkelns periferi kan finna en punkt 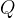 sådan att
sådan att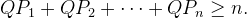

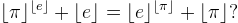
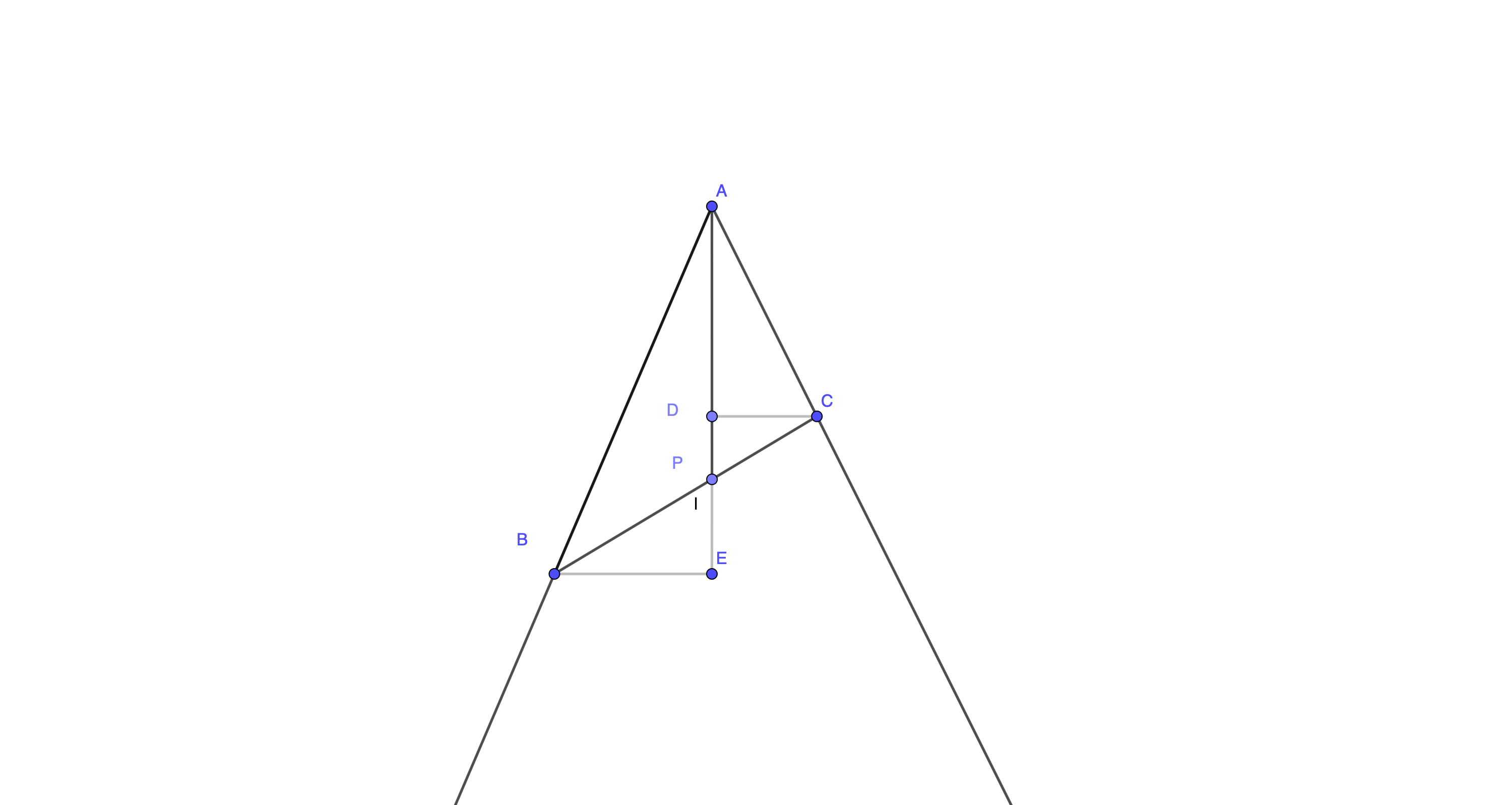
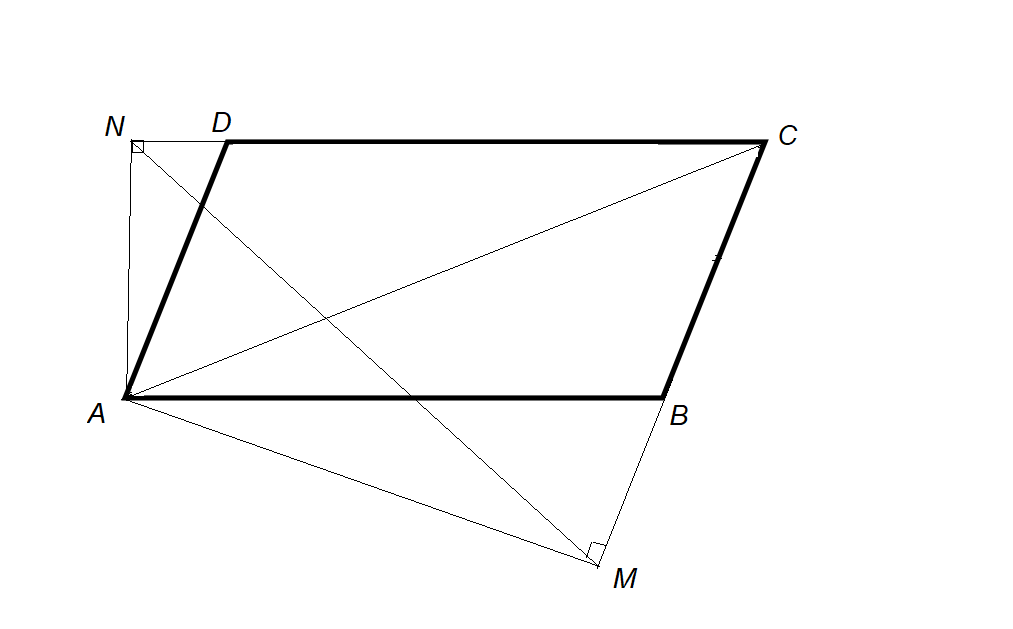
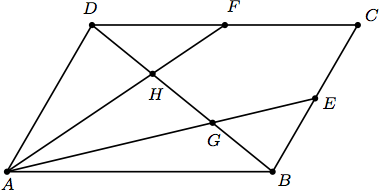
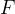 är mittpunkterna på sidorna
är mittpunkterna på sidorna 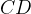 respektive i parallellogrammen
respektive i parallellogrammen 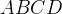 . Visa att sträckorna
. Visa att sträckorna 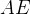 och
och 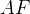 delar diagonalen
delar diagonalen 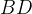 i tre lika långa delar (se figuren nedan), dvs.
i tre lika långa delar (se figuren nedan), dvs. 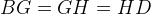 .
. 
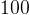
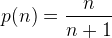
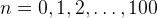
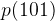

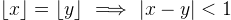 .
Gäller den omvända implikationen?
.
Gäller den omvända implikationen? 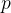 och
och 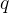 vara två olika primtal. Visa att
vara två olika primtal. Visa att 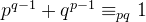 .
.