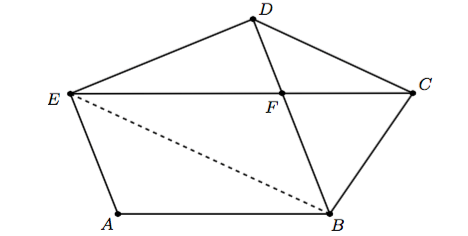
Vi tänker oss att vi har femhörningen som på bilden, där varje diagonal delar femhörningen i en triangel av area ett och en parallellogram. Låt F vara skärningspunkten mellan diagonalerna EC och DB, då får vi parallellogram ABFE som utgörs av två trianglar med area 1 (eller hur?).
Testa och se om det leder någon vart!
/Caroline Mentor
Ahaa okej! Då kan får man |ABFE| = 2 och ur uppgiften vi man att |ECD| = |BDC|=1. Om man skulle addera dessa får man |FDC| två gånger, vilket inte är bra. Jag tänker att man kan subtrahera denna från totalen för att få den rätta arean, men kan inte komma på hur man ska få fram |FDC|. Om EB hade varit parallell med DC hade man kunnat använda likformighet för att få fram propotionen mellan areorna, men detta är inte garanterat.
Får till slut att |ABCDE| = |ABE|+|FBE|+|CED|+|DBC|-|FCD| = 4-|FCD|, och om jag hade kunnat ta fram EF/EC så kan man räkna ut |FCD| genom resonemanget som följer efter Thales sats på sida 69 i kursboken.
Om det finns något annat att peka på hade det uppskattats! (Kanske har jag helt fel approach här uppe??)
Hej!
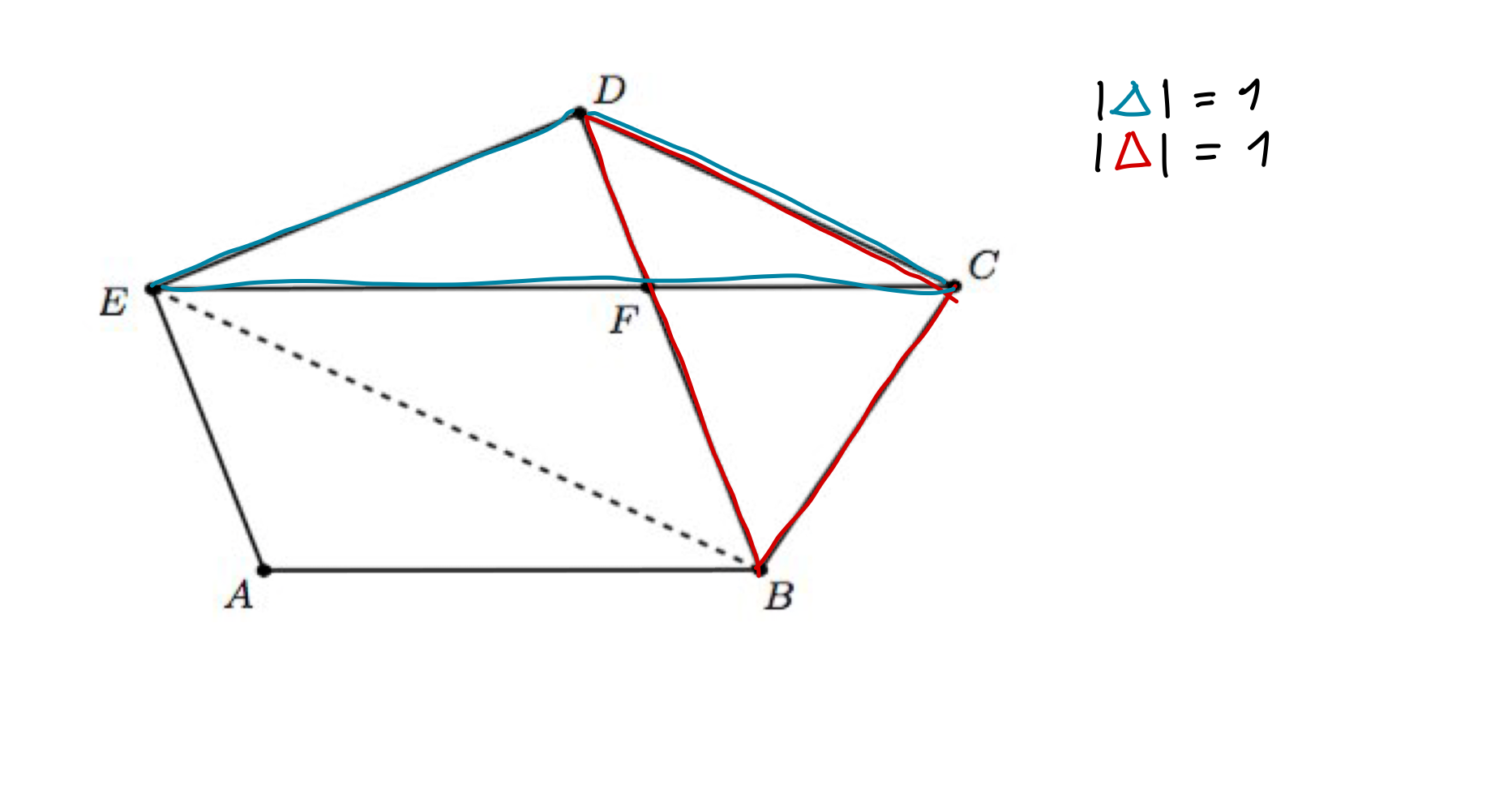
Du tänker helt rätt i att addera dessa areor och sedan dra ifrån arean av |FCD|. I och med att trianglarna DCB och DCE har samma area (från uppgiftsbeskrivningen), och de har samma bas så måste höjden också vara densamma. Det följer av detta att EB och DC är parallella (ser du varför?). Så du kan använda dig av detta för att lösa problemet!
/Caroline, mentor
Jag trodde jag var med, men det jag tänkte göra fungerade inte alls. Provade att fösöka använda lemma 3.1 eller 3.2, men fastnar i att man måste bestämma förhållandet mellan antingen DC och EB eller höjderna från respektive parallella linje till mittpunkten F. Vad jag också förstår är att alla trianglar i parallelltrapetsen är likformiga, men det verkar bara leda till olika förhållande som inte kan lösas.
Till exempel kan man få |DCE|/|BCE| =DF/FB = CF/FE = |DCB|/|DEB| och ett liknande ur lemma 3.1 med höjderna, men det leder ingenvart...
Hade jag kunnat få mer handledning för denna?
Du får från lemma 3.1 också att DF/FB = |DEF|/|BEF|, men |DEF| = |DEC| - |DCF| = 1 - |DCF| (*) och vi har att |BEF| = 1 (från uppgiftsbeskrivningen). Vi har också |DCF|/|DCB| = |DCF|/(1-|DCF|) (**). Från dessa (* och **) kan du få ett uttryck för |DCF|!
/Caroline, mentor
Höjderna blir inte DF och BF i de trianglarna (just för att de inte är vinkelräta mot basen som du säger). Vi vet att DCE och DCB har samma höjd just eftersom DC och EB är parallella, och höjden på dessa trianglar går från DC till EB.
/Caroline, mentor
Ritade om en ny bild för att tydliggöra vad jag (fortfarande) inte förstår. Hur kan lemma 3.1 ge dessa förhållande när det enda satsen ger är förhållandet mellan area och höjd för trianglar med delad bas? Kan det vara på detta vis?:
För trianglarna DEF och BEF är den enda basen de delar EF, och därmed skulle vi få höjder som går från D och B till punkter skilda från F: 
Om man kallar punkterna där respektive höjd möter EC för samma som linjen (h1,h2) kan man argumentera för att h1FD~h2FC enligt VVV. Då får man väll att h1/h2 = DF/FB, är det på detta vis precis likheten tidigare: 
Är detta mellansteget som jag missat/missförstått?
Jag är inte helt säker på hur Caroline har tänkt här men jag tycker att dit resonemang ser ut att vara åt rätt hål. Kan du kanske förtydliga hur du visar att h1FD och h2FB är likformiga? Jag antar att du menar h2FB och inte h2FC eftersom h2FC inte är en triangel. Att två av vinklarna stämmer överens ser man ganska tydligt men varför är vinkel h1DF samma som vinkeln h2BF?
Mentor Jacob