« Gammalt Handledningsforum (Gör ej nya inlägg)

Anonymous User

Algebra 3 uppgift 5

4 replies
Last

Hej, har aldrig jobbat med ekvationer inom heltalsfunktioner, och undrade bara hur man får hantera delen innanför klamrarna.

Lös ekvationerna

(i) 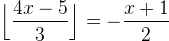\Big \lfloor \dfrac{4x-5}{3} \Big \rfloor= -\dfrac{x+1}{2},

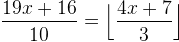(ii) \dfrac{19x+16}{10}=\Big \lfloor \dfrac{4x+7}{3} \Big \rfloor.

4 replies
  1. Post by THEA LI
    Re: Algebra 3 uppgift 5
    Hej!


    Kolla på exempel 12.9 i boken!

    Vänligen,

    Thea

  2. Post by Anonymous User
    Re: Algebra 3 uppgift 5
    Hej, jag har inte tillgång till boken just nu och är utomlands så har ingen möjlighet att beställa den, skulle det vara möjligt för er att skicka en bild eller transkribera exempel 12.9?
  3. Post by VILLE NORDSTRÖM
    exempel 12.9
    Hej, 


    Här är exemplet. Vi ska lösa ekvationen \(\lfloor \frac{5+6x}{8}\rfloor=\frac{15x-7}{5}.\) Antag att \(x\) är en lösning och  låt \(a=\lfloor \frac{5+6x}{8}\rfloor=\frac{15x-7}{5}.\) Talet \(a\) är ett heltal och ur likheten \(a=\frac{15x-7}{5}\) får vi \(x=\frac{5a+7}{15}\). Likheten \(a=\lfloor \frac{5+6x}{8}\rfloor\) ger oss olikheten \(a\leq \frac{5+6x}{8}\leq a+1\). I olikheten substituerar vi \(x=\frac{5a+7}{15}\) och får \(a\leq \frac{5+6</span><span style="font-size:14.7756px;font-family:'-apple-system', BlinkMacSystemFont;">\frac{5a+7}{15}}{8}\leq a+1\). Efter förenklingar ger den första olikheten \(a≤\frac{39}{30}\) och den andra ger \(-\frac{1}{30}<a\). Eftersom \(a\) är ett heltal måste \(a=0\) eller \(a=1\). Båda dessa värden på \(a\) ger oss en lösning för \(x\).


    Hälsningar,

    Ville

    1 reply
  4. Parent of this post↑ Reply to VNVILLE NORDSTRÖM from Anonymous User
    Re: exempel 12.9
    Tack så hemskt mycket.
Older discussion
Newer discussion