Post by RODI KAY
Visa att det inte finns någon punkt 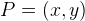 med heltalskoordinater som ligger på parabeln
med heltalskoordinater som ligger på parabeln 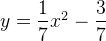 .
.
Jag har helt fastnat på problemet x^2 kongruent med 3 modulus 7. Försökte visa att det inta fanns några lösningar från tal 1-7, samt är det ett primtal sådan att alla tal efter 7 följer samma kongruenta "pattern"
Annars ville jag visa x^2-3 kongruent med 0 (mod 7) . Dvs då detta tal x^2-3 bör vara delbart 7, åtminstone en av faktorerna.
Visa att det inte finns någon punkt 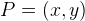 med heltalskoordinater som ligger på parabeln
med heltalskoordinater som ligger på parabeln 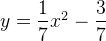 .
.
Du är på rätt spår! Ett tips: Om du multiplicerar båda led med 7 och kastar om termerna lite så får du x^2 - 7y = 3.
Vad måste då gälla för x^2 modulo 7?
Återkom om du fastnar igen!
Mvh,
Nell
Hej,
Tack! Jag antar att jag ska uttrycka det annourlunda än x^2 ≡ 3(mod7)?
Sambandet du anger stämmer! Däremot räcker det inte som svar på uppgiften, du måste motivera varför detta innebär att det inte finns någon heltalspunkt P på den givna parabeln. (Ledtråd: givet ett x, vad kan det anta för värden modulo 7? Och vad innebär det för x^2?)
Mvh,
Nell