Jag har kört fast på detta problem. Uppgiften lyder:
Givet en cirkel med radie 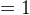 och
och 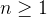 punkter,
punkter, 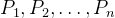 . Visa att man på cirkelns periferi kan finna en punkt
. Visa att man på cirkelns periferi kan finna en punkt 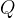 sådan att
sådan att
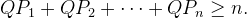
Jag har försökt bilda fyrhörningar med Pn, Pn+1 Q och cirkelns mittpunkt för att med hjälp av Ptolemaios sats och ledvis addering komma fram. Funkar inte. Har någon en idé?