Nyhetsforum

Digitalträff den 28/3

Digitalträff den 28/3

av Yishao Zhou -
Antal svar: 0

Hej!

Lösningsförslag till Problem 2 och 4 (för fredagen den 21/3) finns på https://utmanande.math.su.se/mod/folder/view.php?id=160

Vi ses den 28/3 som planerad på kl 17 på zoomrum https://stockholmuniversity.zoom.us/j/64826157501. Meddela gärna mig om du vill komma annars ställer jag in om jag inte får något på torsdag kväll. 

Till den kommande träffen diskuterar vi ämnen från Kapitel 15. Som vanligt föreslår jag några problem som underlag för diskussionen.

1.  Om 10 personer vardera skakar hand med varandra, hur många handslag ägde rum? Vad har denna fråga med grafteori att göra?

2. Bland en grupp på 5 personer, är det möjligt för alla att vara vänner med exakt 2 av personerna i gruppen? Vad sägs om 3 av personerna i gruppen?

3. För var och en av följande, försök att ge två olika grafer med de givna egenskaperna, eller förklara varför det är omöjligt att göra det.

  • Två olika grafer med 8 hörn alla av grad 2.
  • Två olika grafer med 5 hörn alla av grad 4.
  • Två olika grafer med 5 hörn alla av grad 3.
4. Vilka (om någon) av graferna nedan är desamma? Vilka är olika? Förklara. 
    Vilken av graferna  innehåller Eulerstig eller kretsar? Vilka av graferna är planära?


5. (i) Rita en graf som har en Euler-krets men inte är planär. 
    (ii) Rita en graf som inte har en Eulerstig och inte heller är planar.

6. Antag att G är en graf med \(n\) hörn, var och en med grad 5.
  •  För vilka värden på \(n\) är detta meningsfullt?
  • För vilka värden på \(n\) har grafen en Eulerstig?
  • Vilket är det minsta värdet på \(n\) för vilken kan grafen vara planär?
7. På en skoldans turas 6 tjejer och 4 killar om att dansa (som par) med varandra.
  • Hur många par dansade om varje tjej dansar med varje pojke?
  • Hur många par dansade om alla dansade med alla andra (oavsett kön)?
  • Förklara vilka grafer som kan användas för att representera dessa situationer.
8. Betrakta
 

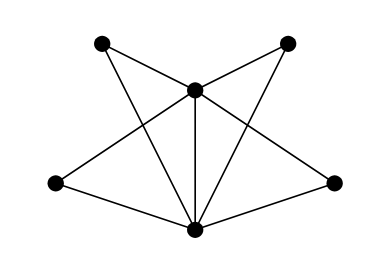
  • Har grafen en Eulerstig eller krets? Förklara.
  • Är grafen plan? Förklara.
  • Är grafen bipartite? Komplett? Komplett bipartie?
9. För varje del nedan, säg om påståendet är sant eller falskt. Förklara varför de sanna påståendena är sanna och ge motexempel på de falska påståendena.

  • Varje bipartite graf är planär.
  • Varje bipartite graf har en Eulerstig.
  • Varje hörn av en bipartite graf har jämn grad.
  • En graf är bipartite om och endast om summan av graderna av alla hörn är jämn.
Trevlig helg!
Yishao