Hej!
Två av problemen vi diskuterade i fredags finns nu i mappen https://utmanande.math.su.se/mod/folder/view.php?id=160
Vi ses på zoom
Till den kommande fredag behandlar vi kapitel 2, 5 & 12. För att kunna ha en effektiv diskussion föreslår jag följande problem.
1. Låt \(x\) vare ett reellt tal. Vi definierar golvfunktion (eller heltalsdelen) \(\lfloor x\rfloor\) som det entydiga heltalet \(n\) som uppfyller \(n\le x<n+1\).
(a) Varför är \(\lfloor{x}\rfloor\) väldefinierad? Dvs varför ett sådant \(n\) existerar och varför är det entydigt? (vi diskuterar bara fallet \(x\) är ett rationellt tal.
(b) Är termen heltalsdelen tillräckligt tydligt?
(c) Kan vi använda det för att beskriva avrundning av ett reellt tal? Hur?
(d) Visa följande egenskaper med definitionen ovan.
- Låt \(m\) vara ett heltal och \(x\) ett reellt tal. Då gäller \(m\le x\) om och endast om \(m\le \lfloor{x}\rfloor\).
- Låt \(x\) vara ett reellt tal. Då är \(\lfloor{x}\rfloor\) det största heltal som är mindre eller lika med \(x\).
- Låt \(m\) vara ett heltal. Då \(\lfloor{m}\rfloor=m\).
- Låt \(x\) vara ett icke-negativt reellt tal. Då \(\lfloor{x}\rfloor=\displaystyle\sum_{\begin{smallmatrix}m\le x\\m \text{ icke-negativa heltal}\end{smallmatrix}}1\).
- Balanserade parenteser: Vi har \(n\) par av parenteser och vi vill gruppera dem. Vi ska sätta ut parenteser så att en öppenparentes ska matcha en slutparentes. Här är några exempel:

- Bergskedjor: Hur många bergkedjor finns det som är konstruerade så att det finns \(n\) uppförsbackar och \(n\) nedförsbackar av en viss längdenhet?

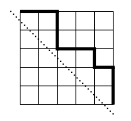
- Diagonal-undvikande vägar: Vi har en kvadrat med \(n\times n\) rutor. Hur många vägar av längd \(2n\)
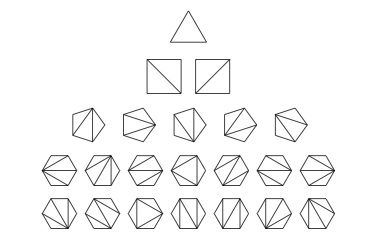
- Triangularisering av månghörning: Hur många sätt kan vi dela upp en \(n+2\)-hörning i trianglar (vi får bara använda sidor och diagonaler)?
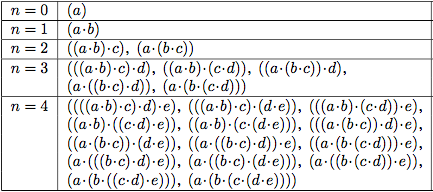
- Multiplikationsordningar Vi har \(n+1\) tal att multiplicera, det vill säga det finns \(n\) multiplikationer. Vi får inte byta ordning av talen men vi kan multiplicera på många sätt. Nedan är de möjliga multiplikations\-ordningarna för \(0\le n\le 4\). Grupperingen markeras med parenteser och \(\cdot\) för multiplikation.
Hitta en formel för antalet möjligheter för alla dessa problem antingen sluten form eller rekursivformel.
Yishao