Låt H vara ortocentrum (skärningspunkten mellan höjderna) i triangel ABC. Cirkeln med medelpunkt i H som går genom punkten C skär sidorna AC och BC, eller deras förlängningar, i punkterna E respektive D (se figuren nedan).
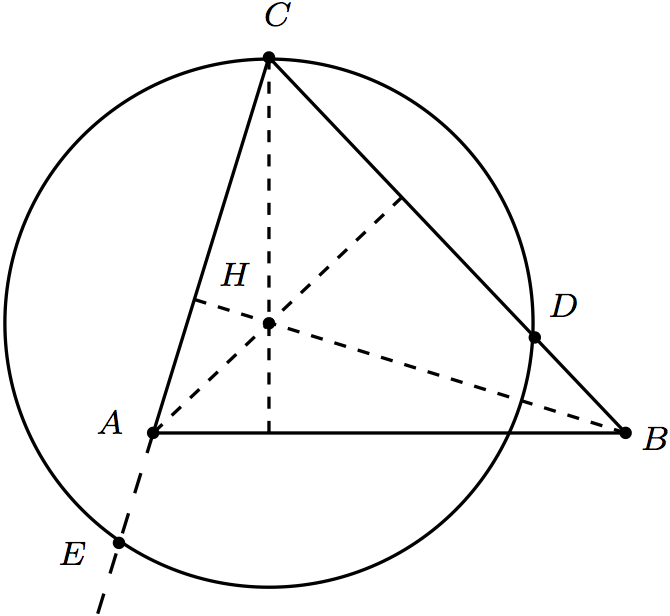
Visa att punkterna B, D, H, A och E ligger på en cirkel.
Ledtråd: Visa att vinkeln CAH=HDE och att fyrhörning DHAE är cyklisk.
Har suttit med denna uppgift jätte länge och fattar verkligen inte vad jag skall göra. Läst i bokens kapitel flertal gånger men det tar mig ingen vart. Vet inte hur jag skall bevisa att vinklarna CAH=HDE. Skulle vara jätte uppskattat med hjälp. Vilka satser jag skall använda, känns som det är något jag missar.