Post by Anna Lindeberg
Uppgiften består (som jag tror att du förstått från ovan) av två delar: bevisa den givna implikationen, och sen besvara frågan antingen med ett bevis, eller ett motexempel.
För att bevisa att implikationen gäller, behöver du visa att för varje tal x och y som uppfyller ⌊x⌋=⌊y⌋, så kommer det gälla att |x-y|<1. Om du tycker det är klurigt att starta så tipsar jag om att fundera över definitionen av ⌊x⌋och⌊y⌋.
Den andra frågan undrar om det gäller att |x-y|<1 => ⌊x⌋=⌊y⌋. Det vill säga: om du vet att talen tal x och y uppfyller att |x-y|<1, vet du då att ⌊x⌋=⌊y⌋? Antingen behöver du bevisa att så är fallet (likt i första deluppgiften), eller så kan du ge ett exempel på faktiska tal x och y så att |x-y|<1 men ⌊x⌋=/=⌊y⌋ –– ett motexempel alltså!
Hoppas detta förtydligar situationen, annars finns vi mentorer här och besvarar följdfrågor. Lycka till!
Vänligen,
Anna
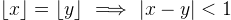 .
Gäller den omvända implikationen?
.
Gäller den omvända implikationen?