Hej!
Tack alla som deltog i seminariet. Här är dom som jag noterade var med:
- Eskil Sandblom
- Noa Bengtsson
- Oscar Sillén
- Tove Tiedemann
- Gustav Klintberg
- Liv TW
- Raquel Castenada
- Tomas Heimdal
- Gustav Ekerud
- Lukas W
- Per Karlsson Kremer
- Sofia Cellini
Om ni saknas får ni gärna maila oss på utmanande-matematik@math.su.se.
Lösning till Problem 1
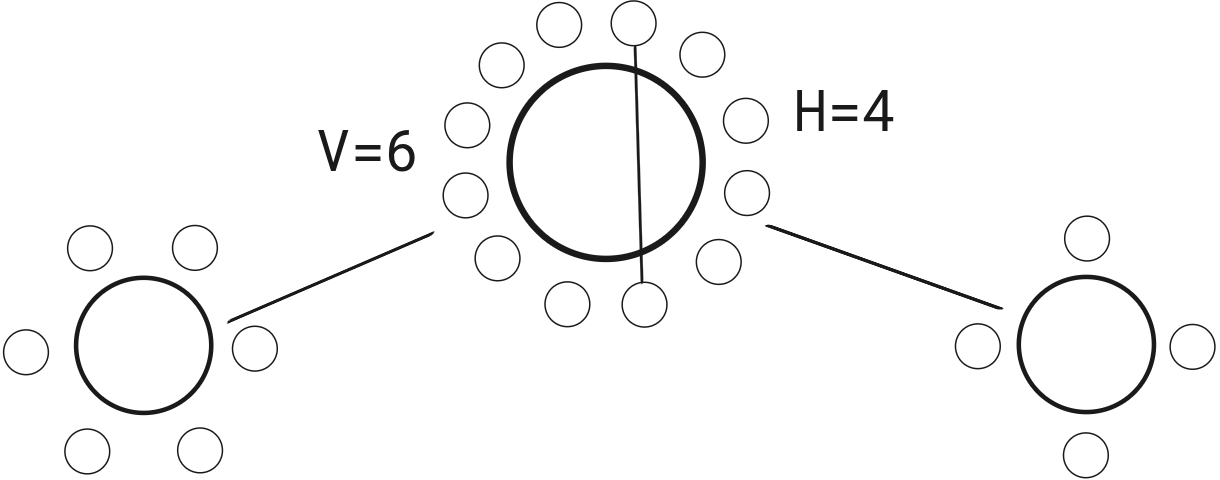
Betrakta det mer generellt att vi har \(2n\) personer som ska delas in i \(n\) par som skakar hand utan att något pars armar korsar något annat pars armar. Kalla antalet sätt detta kan ske på för \(S(2n)\). När ett par skakar hand över bordet så kommer bordet att delas in i två sidor, en vänstersida och en högersida, bestående av \(V\) personer och \(H=2n-2-V\) personer. Detta kan ses som två underproblem där nu dessa resterande personer ska delas in i \(V/2\) och \(H/2\) par respektive som skakar hand utan att något pars armar korsar något annat pars armar. Se följande bild.
[Bild]
Eftersom det måste vara ett jämnt antal personer för att alla ska ha någon att skaka hand med så räcker det att betrakta fallen \(V=0,2,4,\dots,2n-2\). Sammantaget får vi ekvationen
\(S(2n)=\sum_{k=0}^{n-1}S(2k)S(2n-2-2k).\)
För \(2n=12\) behöver vi alltså räkna ut
\(S(0)S(10)+S(2)S(8)+S(4)S(6)+S(6)S(4)+S(8)S(2)+S(10)S(0)=2(S(0)S(10)+S(2)S(8)+S(4)S(6)).\)
Vi har att \(S(0)=1\) och \(S(2)=1\), så vi kan nu använda ekvationen för att räkna ut
\(S(4)=S(0)S(2)+S(2)S(0)=2\)
och
\(S(6)=S(0)S(4)+S(2)S(2)+S(4)S(0)=5,\)
\(S(8)=S(0)S(6)+S(2)S(4)+S(4)S(2)+S(6)S(0)=14\)
\(S(10)=S(0)S(8)+S(2)S(6)+S(4)S(4)+S(6)S(2)+S(8)S(0)=42\)
och slutgiltigen
\(S(12)=2(S(0)S(10)+S(2)S(8)+S(4)S(6))=132.\)
Svar: Därmed är antalet sätt som \(12\) personer kan skaka hand over ett runt bord utan att korsa varandras händer \(132\).
Extra: talen i talföljden \(1,1,2,5,14,42,132,...\) kallas för Catalantalen (se bevis här [Handshakes Across a (Round) Table]) och förekommer i otroligt många kombinatoriska problem. Minst 214 olika problem har dessa som sin generella lösning (se boken Catalan Numbers av Richard P. Stanley). De har en sluten formel
\(S(2n)=C_n=\frac{1}{n+1} {2n\choose n}.\)
Lösning till Problem 2
Sida 11 av [IMO2022 Shortlisted Problems with Solutions]
Lösning till Problem 3
Sida 3 av [52nd Austrian Mathematical Olympiad Junior Regional Competition—Solutions]