Hej alla!
Här kommer Zoomlänk och problem till nästa seminarium, 13:00 på fredag.
https://stockholmuniversity.zoom.us/j/61224350018
Källor och lösningsförslag kommer efter seminariet.
Problem 1
12 personer sitter jämt fördelade kring ett cirkulärt bord där alla kan nå alla andra personer. Hur många sätt kan gruppen delas in i 6 par som skakar hand över bordet, utan att något pars armar korsar något annat pars armar?
Tips: Hur skulle en generalisering av problemet se ut?
Problem 2
Hitta alla funktioner \(f\) från positiva reella tal till positiva reella tal \(f:\mathbb{R}_{>0}\to\mathbb{R}_{>0}\) så att för varje \(x>0\) finns det ett *unikt* \(y>0\) så att \(xf(y)+yf(x)\leq2\).
Tips: (1) Det finns endast en sådan funktion \(f\).
(2) Vidare, givet en godtycklig funktion 𝑓, introducera en relation "bra" som säger att ett talpar \((x,y)\) är "bra" omm \(xf(y)+yf(x)\). Frågan kan nu omformuleras. Vad för egenskaper har ett "bra" talpar? Vilka slags talpar kan vara "bra"?
Problem 3
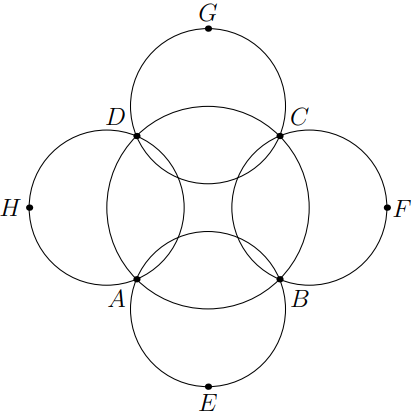
Åtta punkter A, B, C, D, E, F, G, H placeras ovanpå 5 överlappande cirklar som bilden nedan.
Målet är att tilldela vardera av dessa åtta punker en unik siffra 1-8 sådant att för vardera av dessa 5 cirklar är summan av siffrorna på cirkeln densamma som alla andra cirklar.
På hur många sätt kan detta mål uppfyllas?